


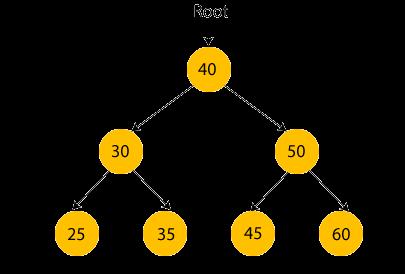
Introduction - Binary Search Tree ek special type ka binary tree hai jisme har node ke left side wale subtree ke sabhi nodes chhote hote hain root node se, aur right side wale subtree ke nodes bade hote hain. Yeh structure aise banaya jata hai taaki searching, insertion, aur deletion ka process efficient ho sake.
Basic Operations in BST:
1. Searching: BST mein searching kaafi fast hoti hai kyunki hamesha ek path follow hota hai. Jab hume koi value search karni hoti hai, toh pehle root node ko check karte hain. Agar root node se chhoti value ho toh left subtree mein jaate hain, aur agar badi ho toh right subtree mein jaate hain. Is tarah se hume ek specific element ka search time log(n) hota hai, jaha n total number of nodes hai. Ek example se samajhte hai agar tree kuch aisa hai:
50
/ \
30 70
/ \ / \
20 40 60 80
Ab agar hume 40 search karna hai, toh pehle root (50) check hoga, fir 40 chhota hai toh left mein jaayenge, fir 30 check hoga, 40 bada hai toh right mein jaayenge, aur hume 40 mil jayega.
2. Insertion: BST mein new element insert karte waqt hume same rule follow karna padta hai. Agar new value root node se chhoti hai toh left subtree mein insert karenge, aur badi hai toh right subtree mein.
Example: Agar hume 65 insert karna ho, toh 50 se bada hai toh right mein jaayenge, fir 70 se chhota hai toh 60 ke right mein insert karenge.
3. Deletion: BST se koi node delete karna thoda tricky hota hai. Teen cases hote hain:
Balanced vs Unbalanced BST :- Ek balanced BST mein left aur right subtree ke height mein zyada fark nahi hota. Agar tree balanced ho, toh saari operations ki time complexity log(n) hoti hai. Lekin agar tree unbalanced ho jaaye, jaise ek skewed tree ban jaye, toh worst case mein searching, insertion, aur deletion ki time complexity O(n) ho jaati hai.
1. Skewed Tree Example (Unbalanced):
10
\
20
\
30
Yahan sab nodes ek side mein hain, isliye yeh ek unbalanced tree hai. Isme searching slow ho jaati hai.
2. Balanced Tree Examples:
AVL Tree: Yeh ek self-balancing BST hota hai jisme har node ka height difference (balance factor) -1, 0, ya 1 hota hai. Agar kabhi insertion ya deletion se tree imbalance ho jaaye, toh rotations ke through balance kiya jaata hai.
Red-Black Tree: Isme har node ko red ya black color assign hota hai aur rules follow kiye jaate hain taaki tree balanced rahe.
BST ka Time Complexity:-
1.Best Case (Balanced Tree) - O(log n)
2.Worst Case (Unbalanced Tree) - O(n)
Iska matlab agar tree balanced ho, toh hume searching, insertion, aur deletion efficiently karne mein time lagta hai, lekin agar tree unbalanced ho jaaye toh performance degrade ho jaati hai.
Real-World Applications of BST:
1.Databases: Searching aur indexing ke liye BST ka use hota hai, jisme hume records ko efficiently access karna hota hai.
2.Compiler Design: Symbol tables ko manage karne ke liye BST ka use hota hai.
3.File Systems: File hierarchies ko organize karne ke liye BST kaafi useful hota hai.
4.Memory Allocation: Dynamic memory allocation algorithms BST ka use karke free memory blocks ko track karte hain.
BST vs Other Data Structures: BST ko Hash Table aur Heap ke saath compare karein toh BST sorted data ko maintain kar sakta hai, jo hash tables mein possible nahi hota. Lekin hash tables searching mein BST se fast hote hain. Heap ka use jab min ya max element ko fast retrieve karna ho tab hota hai, lekin heap mein sorted order maintain nahi hoti.
Toh finally Binary Search Tree ek powerful data structure hai jo searching, sorting, aur dynamic data ke efficient management ke liye kaafi useful hota hai. Agar tree balanced rahe toh performance excellent hoti hai, lekin unbalanced tree se performance degrade ho sakti hai.